Éxito = talento + suerte
Gran éxito = un poco más de talento + un cúmulo de suerte
En su libro pensar rápido, pensar despacio, psicólogo y premio nobel de economía Daniel Kahneman plantea esta ecuación pensando en un torneo de golf de alto nivel.
Suponiendo que un golfista obtiene una muy buena puntuación por encima de la media (aunque en el golf cuantos menos golpes mejor, aquí tomaremos por encima de la media un rendimiento superior), siguiendo la formula, cabria decir que el jugador tiene talento y ha tenido una cuota de suerte aquel día.
Analizando las posibilidades entre ese golfista y otro que no lo ha hecho tan bien podrían surgir dos posibilidades para el siguiente día de competencia:
1- el que lo hizo bien el primer día es probable que vuelva a hacerlo bien, pero un poco menos que la primera vez, ya que tuvo suerte el primer día, y es poco probable que se repita.
2-el que no lo hizo tan bien el primer día, probablemente siga por debajo de la media, pero mejorará ya que su mala suerte posiblemente no siga.

Este patrón estadístico se denomina regresión a la media, es el fenómeno en la cual si una variable es extrema en su primera medición, tenderá a estar más cerca de la media en su segunda medición y, paradójicamente, si es extrema en su segunda medición, tenderá a haber estado más cerca de la media en su primera. El primero en advertirlo fue Francis Galton en el siglo XIX al observar una regresión lineal simple en su articulo: ¨Regression towards mediocrity in hereditary stature¨ comparando la estatura de los padres con la descendencia.
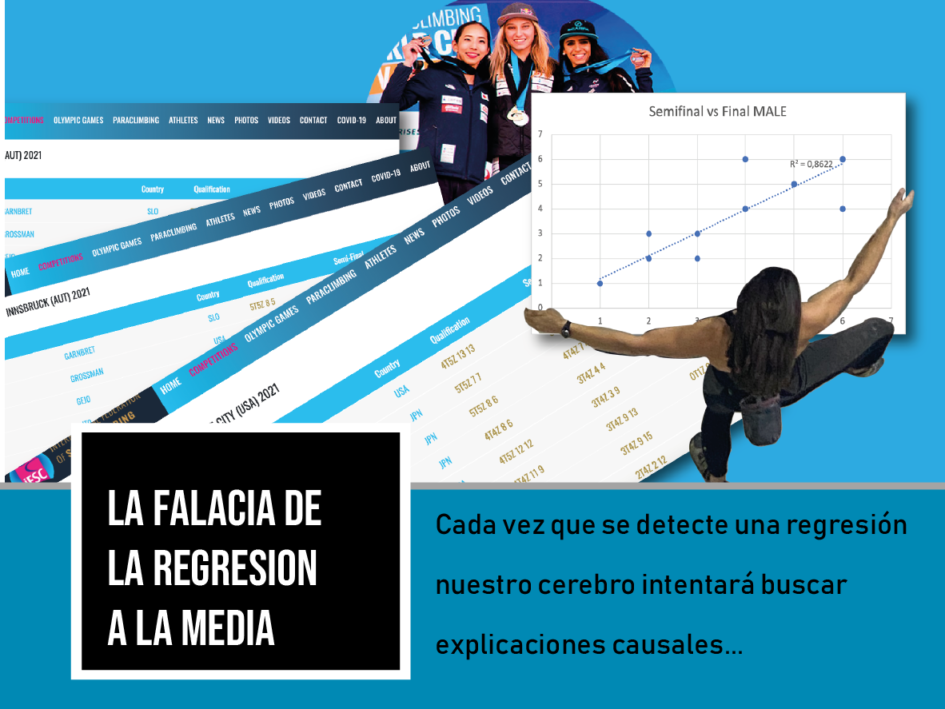
Tomando esta idea me puse a ver este patrón en los finalistas de las cuatro copas del mundo de Boulder disputadas en 2021. Analice el resultado obtenido semifinal comparado con el obtenido en la final. Dibuje los pares de datos en un grafico y obtuve el coeficiente de determinación de los mismos (R²). Los resultados están en las gráficas siguientes, donde el R² para los hombres resulto ser 0,86 y para las mujeres es 0,55.
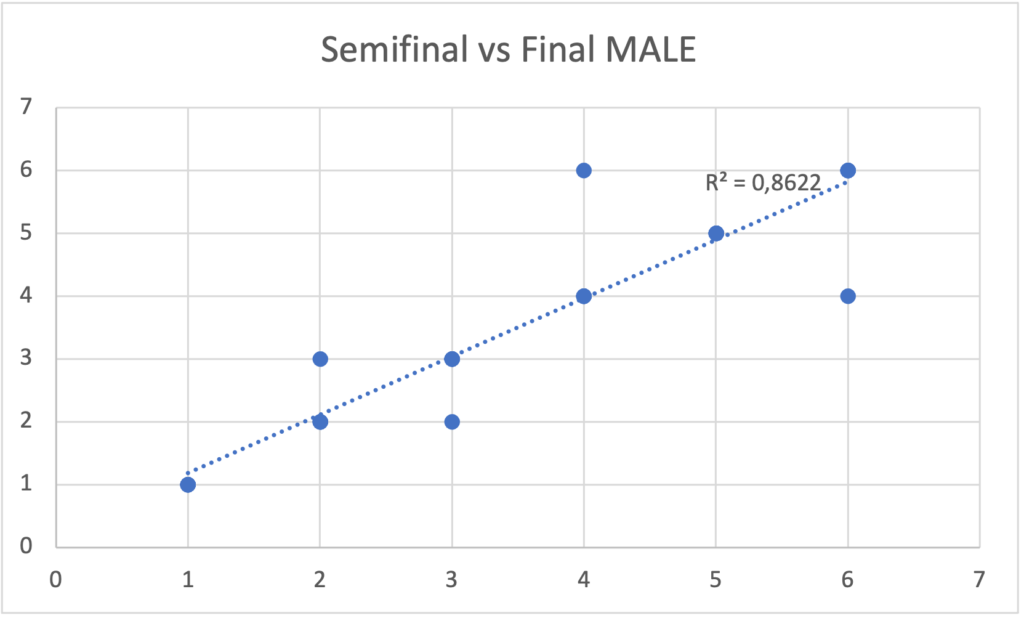
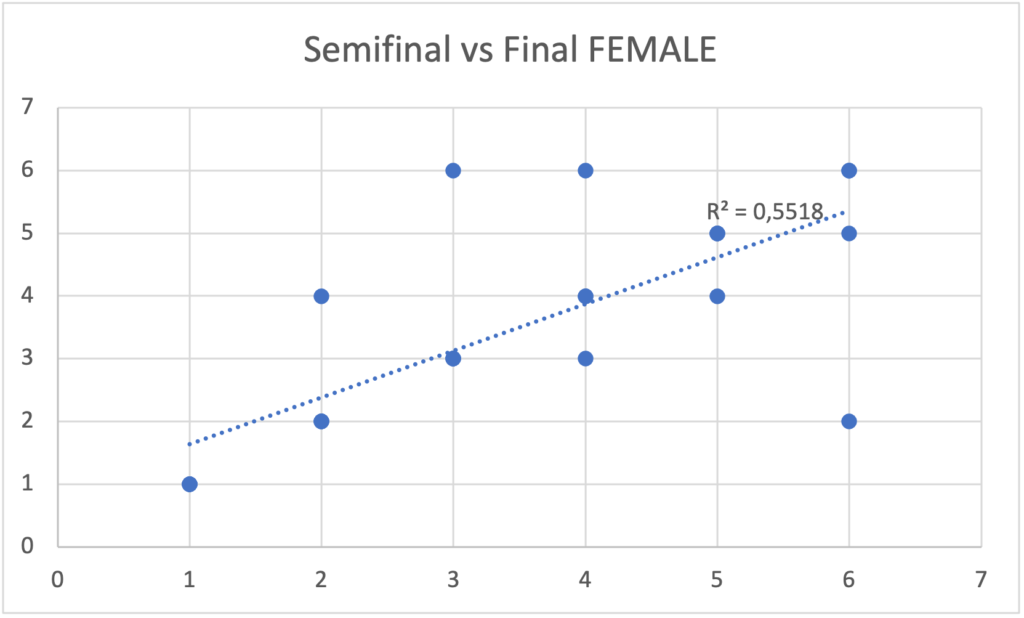
Un R² de 0 indica que el modelo no explica ninguna porción de la variabilidad de los datos de respuesta en torno a su media, mientras que un R² de 1 indica que el modelo explica toda la variabilidad de los datos de respuesta en torno a su media. Es decir que el modelo de los hombres de las posiciones obtenidas en la semifinal explica en un 86% la varianza del resultado en la final, es decir que quienes obtuvieron un buen lugar en la semifinal, es mas probable que obtengan lugar similar en la final. En el caso de las mujeres esa explicación de la varianza se reduce al 55%.
Pero cuando ampliamos este análisis a los resultados de la clasificación en relación a los de la semifinal los datos son bastante distintos, en el caso de los hombres, el R² es de 0,032 y el R² de las mujeres es de 0,30. Definitivamente la diferencia de niveles se hace muy notoria y existe una gran variabilidad en los resultados, casi con una correlación nula para los hombres.
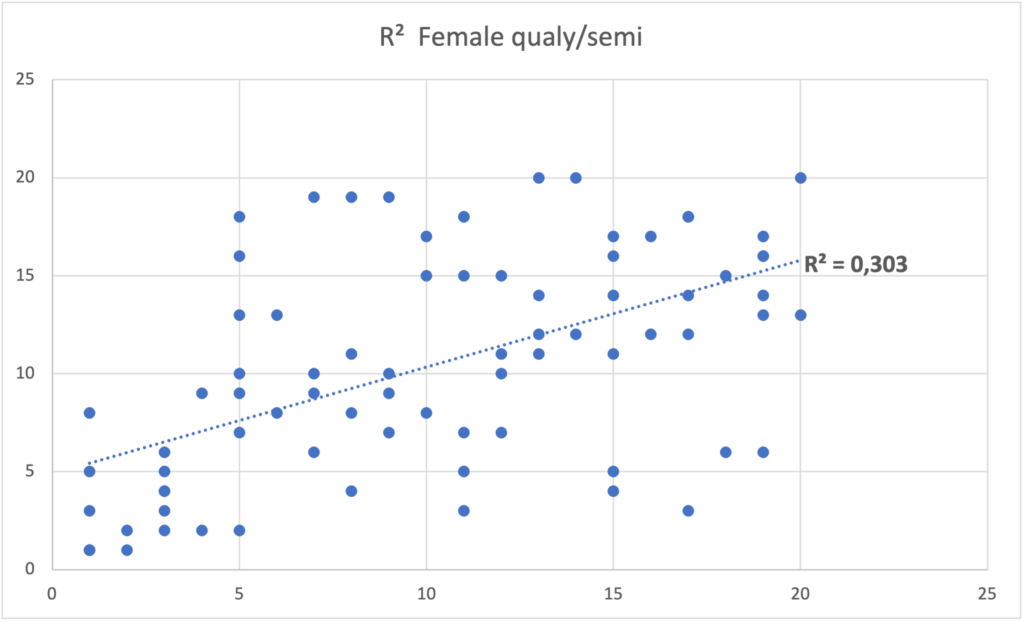
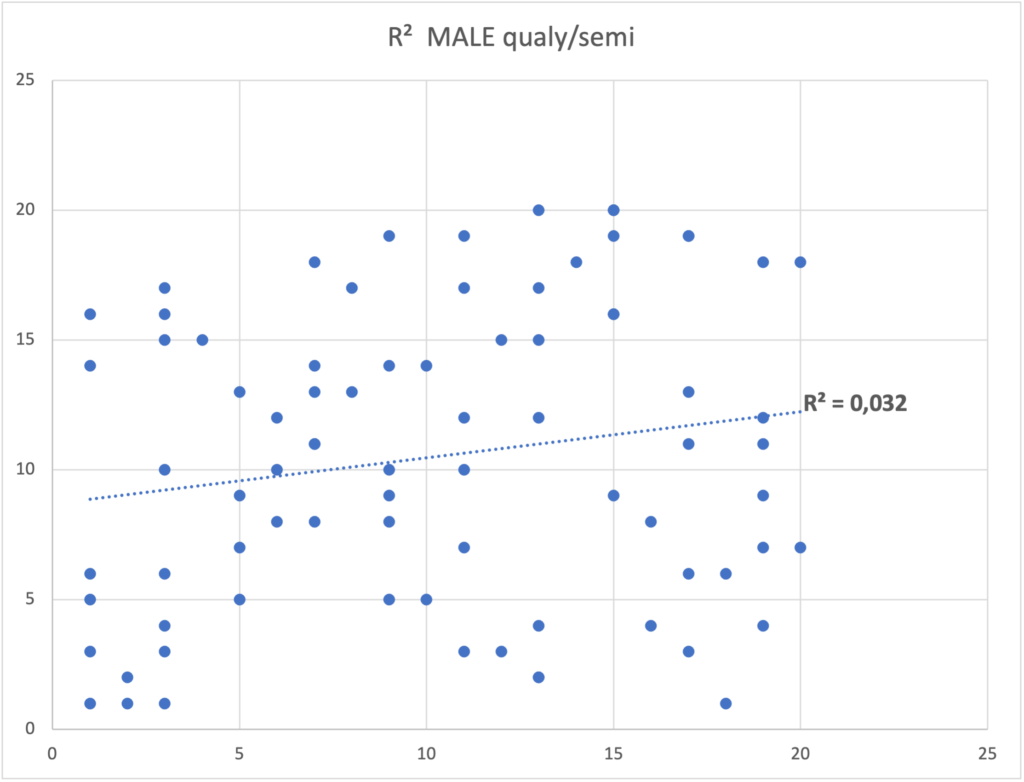
Debemos tener especial cuidado con la regresión a la media al tratar de establecer la causalidad entre dos factores. Cuando la correlación es imperfecta como en el caso de la clasificatoria en relación con la semifinal, lo mejor siempre parecerá empeorar y lo peor siempre parecerá mejorar con el tiempo. Independientemente de cualquier intervención quienes hayan obtenido una mala ubicación en la clasificación obtendrían una mejor ubicación en la semifinal.
Este tipo de razonamiento se inscribe en lo que se denomina falacia de la regresión a la media, que afirma o asume que si un acontecimiento sucede después de otro, el segundo es consecuencia del primero. Este es un error muy común y se define como el hecho de no reconocer la influencia de la regresión y nuestro cerebro tiende a buscar una explicación causal a lo que solo es una regularidad estadística. La secuencia temporal de dos hechos es algo inherente a la causalidad: es verdad que una causa se produce antes de un efecto. La falacia viene de sacar una conclusión basándose solo en el orden de los acontecimientos, lo cual no es un indicador fiable. Es decir, no siempre es verdad que el primer acontecimiento produjo el segundo acontecimiento.
Para ejemplificar esta falacia, Kahneman menciona la conocida maldición de ¨Sports Illustrated¨, una de las revistas mas conocidas en el mundo del deporte. Dicha maldición predice una mala actuación en la temporada siguiente de los deportistas que hayan aparecido en la portada. Para justificar esto se buscan explicaciones como exceso de presión o confianza, pero lo cierto es que para salir en la portada el deportista tiene que haber tenido un rendimiento excepcional, y es de esperarse que el rendimiento de la temporada siguiente no lo sea tanto.
Cada vez que se detecte una regresión nuestro cerebro intentará buscar explicaciones causales, pero la verdad es que la regresión a la media tiene una EXPLICACION, pero no una CAUSA.
Aunque hay algunos ejemplos que parecen contradecir el fenómeno de la regresión a la media: Janja Garnbret y la economía argentina, por mas que tengan un record histórico, en la medición siguiente vuelven a sobresalir.

Referencias:
Kahneman D. (2012). Pensar rápido, pensar despacio. Buenos Aires, Ed Debate, 2021.

Deja un comentario